Por que não podemos dividir por zero?
O veterano comediante Steven Wright brincou que os buracos negros são onde Deus é dividido por zero. Desde que a matemática surgiu há vários milênios, o homem disputou e reformou muitas convenções para manter vivo seu caso de amor com a matemática. Séculos atrás, acreditava a raiz quadrada de números negativos para ser inexistente até Gerolamo Cardano, na 16ªséculo, apresentou ao mundonúmeros complexos, um ramo da matemática que depende inteiramente da raiz quadrada de números negativos.No entanto, existe uma regra ainda a ser quebrada, que é divisão por zero. E se dividir um número por zero é um sacrilégio, talvez um pecado cardinal, qual é o resultado de zero dividido por zero? Se alguém o computasse, o universo imediatamente começaria a colapsar sobre si mesmo? Vamos descobrir por que a operação de dividir por zero é “indefinida” ou, para dizer de forma mais indelicada, “sem sentido”.
É realmente igual ao infinito?
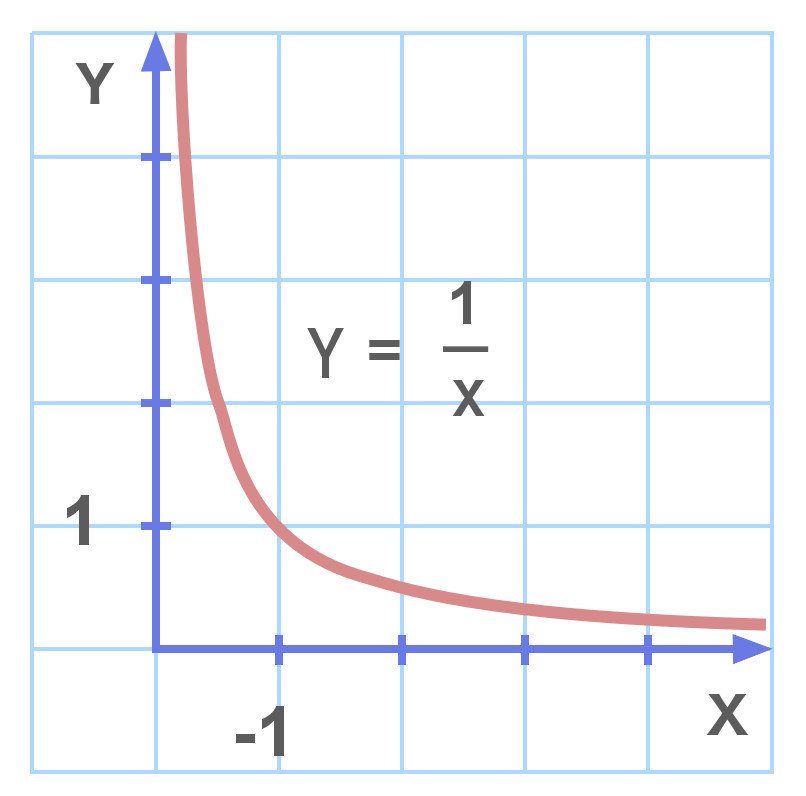
Por conveniência, uma fração na qual o denominador é zero é freqüentemente igualada ao infinito. Este argumento tem algum mérito, considerando a natureza da função inversa. Você provavelmente observou que dividir um número por números menores e menores produz números cada vez maiores. Por exemplo, considere estas frações:
Como os números ficam infinitesimamente menores, a tendência pode ser traçada em direção ao infinito. No entanto,tendendo aoinfinito esendo igual aoinfinito são duas noções muito diferentes. O resultado parece estar a caminho do infinito, mas nunca chega.
O infinito não é um número rígido, mas sim uma ideia; só existe na abstração. No entanto, se tratássemos o infinito como um número distinto e o comparássemos com a fração 1/0, encontraríamos absurdas anomalias matemáticas, particularmente as mais falaciosas de todas as máximas da matemática:
para
Pode-se determinar porque esta fração não tem sentido referindo-se à definição de divisão. A definição mais básica de divisão é, claro, quebrar algo em partes de um certo tamanho. Por exemplo, quando dividimos 20 por dois, o resultado é duas partes de tamanho 10 cada. Então, o que significa dividir 20 por zero? O resultado não é mais partes de um tamanho finito. Ela teria sido finita e muito grande, mesmo quando a dividimos em 0,000000000000001, mas no momento em que a dividimos por zero, a lógica da divisão não é mais preservada e o resultado não é claro.
Outra maneira de definir divisão é como subtração glorificada. O resultado de 100 dividido por 10 é o número de vezes que podemos subtrair 10 de 100 até o resultado ser 0. O resultado, eu espero que você saiba, é 10. No entanto, novamente, dividir 100 por 0 parece ser infinito, como a subtração continua para sempre.
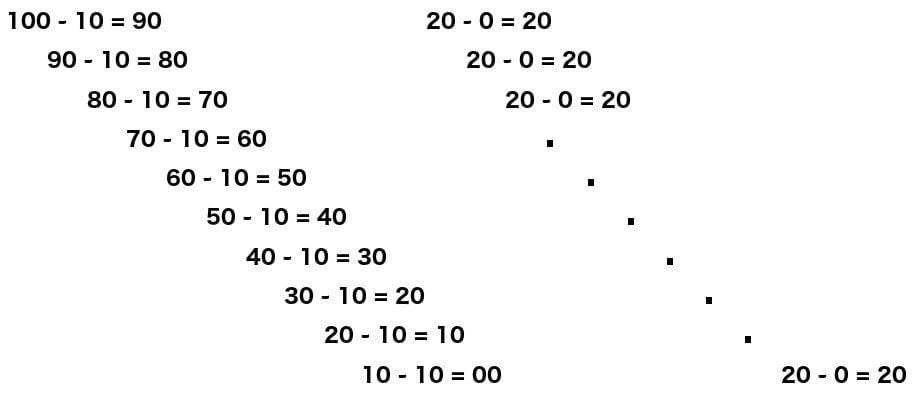
O resultado é, portanto, infinito? Na verdade não. Como mencionado anteriormente, a lógica da operação não é consistente com nossos axiomas. Para verificar se 100 dividido por 10 é realmente 10, podemos adicionar 10 dez vezes para verificar se a soma é realmente 100, o que é. Nós simplesmente adicionamos o número sendo subtraído o número de vezes que obtivemos da divisão. Portanto, para verificar se 100 dividido por 0 é infinito, devemos adicionar zero vezes infinitas. No entanto, como a soma 0 + 0 + 0 +… poderia ser igual a 100?
Isso nos leva à nossa segunda pergunta.
O que é 0/0?
Vamos supor que o resultado não seja infinito, mas sim um valor finito, que denotaremos com ‘x’. A operação então implica que x multiplicado por 0 é 100, o que é tão ridículo quanto as contradições que obtivemos na seção anterior.
O que não é contraditório e ilógico é a afirmação de que qualquer coisa multiplicada por zero é zero. Assim, a equação assume então a seguinte forma:
Isso pode ser reconfigurado e escrito como:
Observe como isso é verdade paraqualquervalor de x. Não importa se x é um número inteiro, número racional, número inteiro ou complexo. Isso é atroz, considerando que, para ser verdade, não apenas um deve ser igual a dois, mas um também deve ser igual a todos os outros números que existem! As infinitas contradições fazem com que todo o sistema numérico se desintegre e o universo imediatamente comece a se desmoronar!
Embora seja fisicamente impossível alcançar isso, os matemáticos dizem que a divisão é “indefinida” porque é contraditória ou paradoxal. A matemática é lógica, como um intrincado castelo de cartas. A consistência de uma estrutura depende da consistência da estrutura abaixo dela, que depende da consistência da estrutura abaixo dela. Essencialmente, toda a estrutura é construída na primeira estrutura, digamos, 1 + 1 = 2. A divisão por zero contradiz o princípio mais fundamental em si.