Por que o Factorial de Zero é igual a um?
A consulta é uma reminiscência deporque um número elevado ao zero de energia é igual auma consulta que eu resolvi em um artigo anterior.Além disso, deixe-me tranquilizar o que tenho anteriormente assegurado ao explicar esse fato óbvio, descaradamente assumido, ainda inexplicável – a relação não é arbitrária.
Existem três maneiras de delinear por que o fatorial de zero é igual a um.
Complete o padrão
O fatorial de um númeroné o produto de todos os números a partir de um até alcançarn.A operação é denotada por um ponto de exclamação que sucede o número cujo fatorial queremos procurar, de modo que o fatorial de n seja representado porn !.Numericamente, as trilhas da multiplicação podem ser ilustradas desta maneira:
1! = 1 * 1 = 1
2! = 1 * 2 = 2
3! = 1 * 2 * 3 = 6
4! = 1 * 2 * 3 * 4 = 24
.
.
.
Se, (n-1)! = 1 * 2 * 3 * 4 … (n-3) * (n-2) * (n-1)
Então, logicamente, n! = 1 * 2 * 3 * 4 … (n-3) * (n-2) * (n-1) * n
Ou, n! = n * (n-1)! – (Eu)
Se você olhar essas trilhas cuidadosamente, um padrão se revelará. Vamos completá-lo até conseguir resultados legítimos:
4! / 4 = 3!
3! / 3 = 2!
2! / 2 = 1!
1! / 1 = 0!
Ou, 0! = 1
Pode-se chegar a este resultado simplesmente conectando 1 para ‘n’ em (i) para obter:
1! = 1 * (1-1)!
1 = 1 * 0!
Ou, 0! = 1
No entanto, esta explicação não nos diz sobre o fato de os fatoriais de números negativos não podem existir. Vamos voltar para o nosso padrão novamente para descobrir o porquê.
.
.
2! / 2 = 1!
1! / 1 = 0!
0! / 0 = … uh-oh
Eu concordaria que esses métodos são um pouco suspeitos; são maneiras aparentemente astutas eimplícitasde determinar o fatorial de zero. É como argumentar afavor deum homem de palha. No entanto, pode-se encontrar uma explicação em um campo cuja existência inteira depende do cálculo de fatoriais – combinatória.
Arranjos
Ele era conhecido tão cedo quanto o 12 º século que existemn!maneiras de organizarnnúmero de objetos diferentes. Este ato de organizar objetos é conhecido como permutação. Deixe-me dar-lhe um exemplo simples para explicar por que existemn!maneiras de organizarnobjetos.
Considere 4 cadeiras que devem ser ocupadas por 4 pessoas. A primeira cadeira pode ser ocupada por qualquer uma dessas quatro pessoas, de modo que o número resultante de escolhas seja 4. Agora, uma cadeira está ocupada, temos 3 opções que são potenciais ocupantes para a próxima cadeira. Da mesma forma, a próxima cadeira apresenta duas escolhas, e a última cadeira apresenta uma única escolha; Está ocupado pelo último homem de pé. Portanto, o número total de escolhas que temos são 4x3x2x1 ou 4 !. Ou, pode-se dizer que existem 4! maneiras de organizar 4 cadeiras distintas.
Assim, quando o valor de ‘n’ é igual a zero, a questão se traduz em quais são as diferentes maneiras pelas quais se pode organizarumnúmerozerode objetos? Um, claro! Há apenas uma permutação ou uma maneira de arrumarnadaporque não há nada para se organizar. O QUE? Honestamente, isso pertence a um ramo da filosofia, embora seja uma das noções desagradáveis ou falsas em que os calouros pontificam depois de ler as citações de Nietzsche em Pinterest.

Consideremos um exemplo que envolva objetos físicos, como pode ser para uma melhor compreensão. Os fatoriais também são centrais para as combinações de computação – um processo que também determina arranjos, mas ao contrário da permutação, a ordem das coisas é irrelevante. A diferença entre permutação e combinação é a diferença entre um bloqueio codificado e uma tigela com uma mistura de frutas em cubos. Os bloqueios codificados geralmente são erroneamente chamados de “bloqueios de combinação” quando eles deveriam ser chamados de bloqueios de permutação, uma vez que 123 e 321 não podem desbloqueá-lo.
Uma fórmula geral para determinar o número de maneiras em que os objetos ‘k’ podem ser organizados entre ‘n’ lugares é:
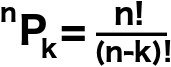
Considerando que, para determinar o número de formas de escolher ou combinar objetos ‘k’ de ‘n’ objetos é:
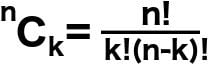
Isso nos permite, digamos, determinar o número de maneiras pelas quais duas bolas podem ser selecionadas de um saco que contém cinco bolas de cores diferentes. Como a ordem das bolas selecionadas não é importante, referimo-nos à segunda fórmula para computar as combinações envolvidas.
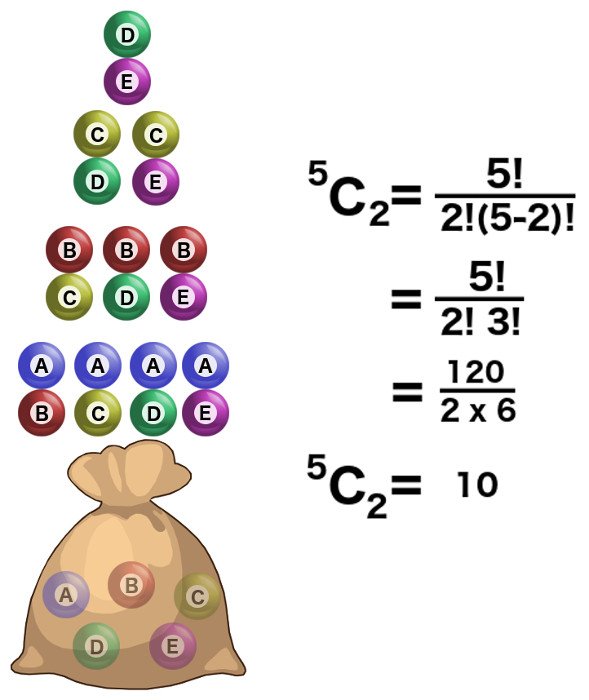
Agora, e se os valores de ‘n’ e ‘k’ forem exatamente iguais? Vamos substituir esses valores e descobrir. Observamos que o fatorial de zero é obtido no denominador.
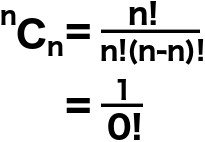
Mas como compreendemos este cálculo matemático visualmente, em termos de nosso exemplo? O cálculo é essencialmente uma solução para uma pergunta que pergunta: qual é o número diferente de maneiras pelas quais podemos escolher três bolas de um saco que contém apenas três bolas? Bem, é claro! Escolhê-los em qualquer ordem não faria a diferença! Equite o cálculo com um e o fatorial de zero gira para ser * rolo de bateria * …… um!